
5 найкращих програм для диспетчеризації вантажних перевезень
Протягом останніх років галузь вантажоперевезень зіткнулася з численними викликами. Від пандемії COVID-19 та пов'язаних з нею обмежень через зменшення обсягів перевезень і зниження тарифів

5 найкращих програм для диспетчеризації вантажних перевезень
Протягом останніх років галузь вантажоперевезень зіткнулася з численними викликами. Від пандемії COVID-19 та пов'язаних з нею обмежень через зменшення обсягів перевезень і зниження тарифів

Розробка додатку для таксі: покроковий процес, функції та проблеми
Коли InDrive вийшов на ринок, здавалося, що після Uber, Bolt і Lyft на ньому не залишилося місця. Але завдяки чіткій бізнес-моделі та сфокусованому, гнучкому продукту компанія зайняла свою нішу і масштабувалася.

Топ-7 систем управління транспортом у 2025
Незалежно від того, наскільки великий ваш бізнес і як довго ви працюєте на ринку, рік за роком ви будете задавати собі одні й ті ж питання, як і кожен власник бізнесу.

10 найпоширеніших ризиків у ланцюгах поставок і як їх уникнути
З 2026 роком на горизонті, геополітика є найбільшим загрозою для глобальних ланцюгів поставок. Війни та політична нестабільність порушують торгові маршрути та ускладнюють логістику по всьому світу.

Покроковий гайд із розробки додатку для доставки посилок на вимогу
Дуже важливо подумати про те, як розробити рішення для задоволення потреб користувачів, залишаючись конкурентоспроможним на ринку, коли ви плануєте створити додаток для доставки посилок.
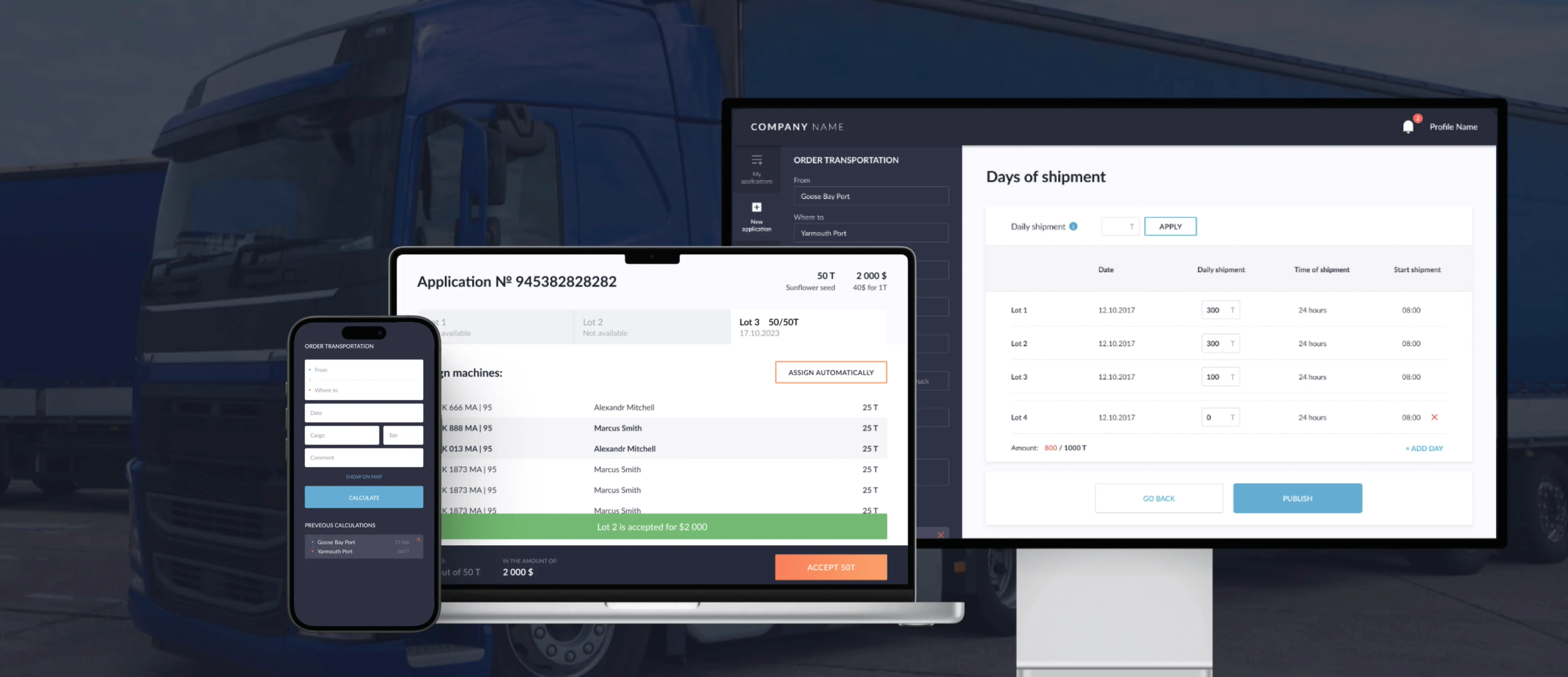
Як створити кастомізовану TMS систему для оптимізації логістики: процеси, етапи
Готові платформи TMS часто обіцяють гнучкість, але спробуйте адаптувати їх до вашого бізнесу, і ви швидко зіткнетеся з труднощами. Диспетчери знаходять обхідні шляхи.

Мандрівники ненавидять стояти в чергах або мати справу з паперовими квитками. Незалежно від того, чи це літак, потяг або автобус, люди очікують, що зможуть забронювати квитки кількома дотиками на своєму телефоні.

Як створити індивідуальну систему управління замовленнями (OMS): витрати, етапи та ключові функції
Розглядаєте можливість створення системи управління замовленнями (OMS)? Тоді ви, напевно, знаєте, що є два варіанти: купити готове рішення (корпоративні варіанти, такі як IBM Sterling OMS, або ніші, такі як Zoho Inventory)

Розробка ERP-систем: як створити індивідуальну ERP для бізнесу
Системи управління підприємством (ERP) стали незамінними за останні два десятиліття. Станом на 2017 рік, 81% організацій впроваджували ERP-програмне забезпечення або завершили впровадження.

Розробка MVP для стартапів: Чому вашому стартапу потрібен MVP?
Dropbox запустився з простого пояснювального відео. Airbnb почав із здачі в оренду надувного матраца. Це були не щасливі випадковості — це були розумно створені MVP.

Розробка додатку для райдшерингу: як створити конкурентоспроможний продукт
Згідно з оцінками, глобальний ринок райдшерінгу, за прогнозами, зросте на $86,33 мільярда протягом 2022-2027 років, прискорюючись зі середньорічним темпом зростання (CAGR) 17,45% до 2027 року. Це означає, що індустрія відновлюється після втрат, спричинених пандемією COVID-19.

Як побудувати систему управління запасами для виробництва
Створення системи управління запасами допомагає компаніям покращити їхнє управління. Вона контролює рівні, знижує витрати та запобігає нестачі або надлишкам товарів. Якщо ви технологічно підкований рітейлер, який не хоче використовувати стороннє програмне забезпечення, ви можете створити просту систему для допомоги у ваших операціях з постачанням.

Моноліт vs мікросервіси: яку архітектуру обрати для вашого продукту
Розробники програмного забезпечення часто дискутують, чи варто використовувати монолітні архітектури чи мікросервіси. Вибір правильних архітектурних патернів є вирішальним для створення масштабованих, підтримуваних і ефективних програмних систем.

Інхаус розробка vs аутсорсинг: що обрати бізнесу
Кожен рік технологічний світ стає складнішим, а потреби великих компаній постійно зростають. Деякі бізнеси вирішують встигати за інноваціями, розбудовуючи власні команди розробників, тоді як інші звертаються до аутсорсингу розробки.

Дизайн-дослідження (UX Research): від розуміння користувачів до кращих продуктів
Занадто часто команди відкладають або знецінюють дизайн-дослідження, вважаючи, що на них немає часу або що вони вже «знають користувача». Водночас багато продуктових команд місяцями розробляють ідеї, щоб зрештою зрозуміти — вони насправді не знають, чого потребують користувачі.